前言

從本章節開始進入進階樹囉，第一個要介紹的是 Min-Max Heap，他是製作 double-ended priority queue 時，可以選擇使用的資料結構。

Min-Max Heap 定義

1. 為 Complete Binary Tree
2. root 層必為 min 層
3. min max 層互相交織
4. 位於 min level 以 x 為 root 之子樹中，x 為最小值
5. 位於 max level 以 x 為 root 之子樹中，x 為最大值
   

Insert X

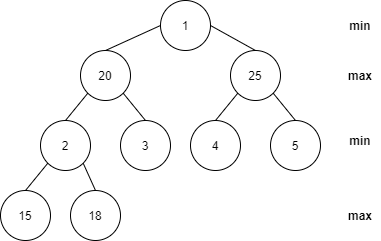
// 若插入點在 max 層，即代表父親位於 min 層
if(x<H[p]){ // x 若比父點小
    H[n] = H[p]; // 把父親往下拉
    verifyMin(x); // 讓 x 去往上挑戰 min
}else{ // x 比父點大
    verifyMax(x); // 讓 x 去往上挑戰 max
}

// 若插入點在 min 層，即代表父親位於 max 層
if(x>H[p]){ // x 若比父點大
    H[n] = H[p]; // 把父親往下拉
    verifyMax(x); // 讓 x 去往上挑戰 max
}else{ // x 比父點小
    verifyMin(x); // 讓 x 去往上挑戰 min
}

Delete

Step 1. 先將 Root 移除
Step 2. 令 X = last node
Step 3. 第三步驟會分為 3 個 cases，準備插入 Root 為空之 Min-Max Heap
Case 1 : root 以下沒子點，x 置入 root
Case 2 : root 以下左右子點為 Min 的話，令 k = min，k 置入 root，x 放入 k
Case 3 : min 位於 root 的子孫的左右子點，令 k = min，令 p = k 的 parent